cdkbook
Graph Properties
Graph theory is the most common representation in cheminformatics, and with
quantum mechanics, rule the informatics side of chemistry. The molecular graph
follow graph theory and defines atoms as molecules and bonds as edge between to
atoms. This is by far the only option, and the IBond allows for more complex
representations, but we will focus on the molecular graph in this chapter.
Partitioning
If one is going to calculate graph properties, the first thing one often has to
do, is to split ensure that one is looking at a fully connected graph. Since
this is often in combination with ensuring fully connected graphs, the
ConnectivityChecker is a welcome tool. It allows
partitioning of the
atoms and bonds in an IAtomContainer into molecules, organized into
IAtomContainerSet:
Script 13.1 code/ConnectivityCheckerDemo.groovy
atomCon = new AtomContainer();
atom1 = new Atom("C");
atom2 = new Atom("C");
atomCon.addAtom(atom1);
atomCon.addAtom(atom2);
moleculeSet = ConnectivityChecker.partitionIntoMolecules(
atomCon
);
println "Number of isolated graphs: " +
moleculeSet.atomContainerCount
Which gives:
Number of isolated graphs: 2
Spanning Tree
The spanning tree of a graph, is subgraph with no cycles; that spans all atoms into a, still, fully connected graph:
Script 13.2 code/SpanningTreeBondCount.groovy
println "Number of azulene bonds: $azulene.bondCount"
treeBuilder = new SpanningTree(azulene)
azuleneTree = treeBuilder.getSpanningTree();
println "Number of tree bonds: $azuleneTree.bondCount"
which returns:
Number of azulene bonds: 11
Number of tree bonds: 9
As a side effect, it also determines which bonds are ring bonds, and which are not:
Script 13.3 code/SpanningTreeRingBonds.groovy
ethaneTree = new SpanningTree(ethane)
println "[ethane]"
println "Number of cyclic bonds: " +
ethaneTree.bondsCyclicCount
println "Number of acyclic bonds: " +
ethaneTree.bondsAcyclicCount
azuleneTree = new SpanningTree(azulene)
println "[azulene]"
println "Number of cyclic bonds: " +
azuleneTree.bondsCyclicCount
println "Number of acyclic bonds: " +
azuleneTree.bondsAcyclicCount
giving
[ethane]
Number of cyclic bonds: 0
Number of acyclic bonds: 1
[azulene]
Number of cyclic bonds: 11
Number of acyclic bonds: 0
Ring counts
Warning: this section needs updating as there are better approaches in CDK 2.x.
Without providing a full review of all ring detection algorithms, this section discusses three algorithms for ring detection. The first two are alternative implementations of the Smallest Set of Smallest Rings (SSSR) concept. While argued to have limited usefulness if not harmful [1], the CDK implements two algorithms: the Figueras algorithm [2], and an improved algorithm addressing limitations of the first [3]. The key limitation is that the resulting set is not unique. Depending on the initial conditions, alternative sets may result for the same structure, particularly for structures with bridgehead atoms. However, on the bright side, it does give some indication on the number of rings in a structure.
The third algorithm discussed is one to find all rings, even if they are merely combinations of smaller rings. For example, naphthalene contains has three rings.
Smallest Rings
The smallest set of smallest rings refers to a set of unique rings that, together, capture all ring atoms. Ring atoms may participate in multiple rings in this set, but each ring will have at least one ring atom not in other rings. But for each compound, the set itself may not be unique. For example, adamantane has multiple SSSRs. The trick of the SSSR algorithm is to find a smallest set of rings that cover all ring atoms.
The CDK implements two algorithms, both are found in the cdk.ringsearch package. The
first is the algorithm developed by Figureas [2] for which the
FiguerasSSSRFinder class can be used:
Script 13.4 code/FiguerasSSSR.groovy
ringset = new FiguerasSSSRFinder().findSSSR(azulene)
println "Number of rings: $ringset.atomContainerCount"
Which tells us the number of smallest rings for azulene:
Number of rings: 2
However, because of this algorithm’s limitations in finding a correct SSSR set for some corner case structure, the following alternative method by Berger et al. [3] is recommended:
ringset = new SSSRFinder(azulene).findSSSR()
println "Number of rings: $ringset.atomContainerCount"
Which calculates the same number of rings for this compound:
Number of rings: 2
All Rings
If you are interesting in all possible rings, you can use the AllRingsFinder class, which
implements an algorithm by Hanser et al. [4]:
Script 13.6 code/FindAllRings.groovy
ringset = new AllRingsFinder().findAllRings(azulene)
println "Number of rings: $ringset.atomContainerCount"
Which returns all three rings present in azulene:
Script 13.6 code/FindAllRings.groovy
ringset = new AllRingsFinder().findAllRings(azulene)
println "Number of rings: $ringset.atomContainerCount"
One should keep in mind that when more smallest rings are fused together, the number of
all rings grows quickly. The AllRingsFinder class has three options to keep the
calculation manageable for larger structures.
The first option is to search only for rings up to a certain size. For example, only rings of at most 5 atoms:
Script 13.7 code/FindUptoFiveRings.groovy
ringset = new AllRingsFinder().findAllRings(azulene, 5)
println "Number of rings: $ringset.atomContainerCount"
For which there is only one in azulene:
Number of rings: 1
A second option is more like a trick to reduce the search space, but first isolating
the ring systems. There are findAllRingsInIsolatedRingSystem alternatives for the
above two approaches.
The third option to limit the execution time is to set a time out. This ensures that a computation will return after a certain time rather than continuing indefinately:
Script 13.8 code/FindAllRingsInLimitedTime.groovy
ringFinder = new AllRingsFinder(AllRingsFinder.Threshold.PubChem_99)
ringset = ringFinder.findAllRings(azulene)
Graph matrices
Chemical graphs have been very successfully used as representations of molecular
structures, but are not always to most suitable representation. For example,
for computation of graph properties often a matrix representation is used
as intermediate step. The CDK has predefined helper classes to calculate two
kind of graph matrices: the adjacency matrix and the distance matrix. Both
are found in the cdk.graph.matrix package.
Adjacency matrix
The adjacency matrix describes which atoms are connected via a covalent
bond. All matrix elements that link to bonded atoms are 1, and those matrix
elements for disconnected atoms are 0. In mathematical terms, the adjacency matrix A is defined as:
Copy back in the equation. MathML?
The algorithm to calculate this matrix is implemented in the
AdjacencyMatrix class. The matrix is calculated with
the static getMatrix(IAtomContainer) method:
Script 13.9 code/AdjacencyMatrixCalc.groovy
int[][] matrix = AdjacencyMatrix.getMatrix(ethanoicAcid)
for (row=0;row<ethanoicAcid.getAtomCount();row++) {
for (col=0;col<ethanoicAcid.getAtomCount();col++) {
print matrix[row][col] + " "
}
println ""
}
This code outputs the matrix, resulting for ethanoic acid, with the atoms in the order C, C, O, and O, in:
0 1 0 0
1 0 1 1
0 1 0 0
0 1 0 0
Distance matrix
The distance matrix describes the number of bonds on has to traverse
to get from one atom to another. Therefore, it has zeros on the diagonal
and non-zero values at all other locations. Matrix elements for
neighboring atoms are 1 and others are larger. The CDK uses
Floyd’s algorithm to calculate this matrix [5],
which is exposed via the TopologicalMatrix class:
Script 13.10 code/DistanceMatrix.groovy
int[][] matrix = TopologicalMatrix.getMatrix(ethanoicAcid)
For the ethanoic acid used earlier, the resulting matrix looks like:
0 1 2 2
1 0 1 1
2 1 0 2
2 1 2 0
Atom Numbers
Another important aspect of the chemical graph, is that the graph uniquely places atoms in the molecule. That is, the graphs allows us to uniquely identify, and therefore, number atoms in the molecule. This is an important aspect of cheminformatics, and the concept behind canonicalization, such as used to create canonical SMILES. The InChI library (see Chapter 20) implements such an algorithm, and we can use it to assign unique integers to all atoms in a chemical graph.
Morgan Atom Numbers
Morgan published an algorithm in 1965 to assign numbers to vertices in the chemical graph [6]. The algorithm does not take into account the element symbols associated with those vertices, and it only based on the connectivity. Therefore, we see the same number of symmetry related atoms, even if they have different symbols. If we run:
Script 13.11 code/MorganAtomNumbers.groovy
oxazole = MoleculeFactory.makeOxazole();
long[] morganNumbers =
MorganNumbersTools.getMorganNumbers(
oxazole
);
for (i in 0..(oxazole.atomCount-1)) {
println oxazole.getAtom(i).symbol +
" " + morganNumbers[i]
}
we see this output:
C 64
O 64
C 64
N 64
C 64
InChI Atom Numbers

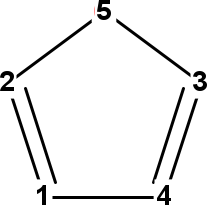
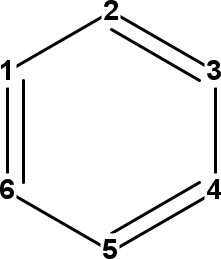
Figure 14.1: InChI atom numbers of adenine (left), oxazole (middle), and benzene (right).
The InChI library does not have a direct method to calculate atom numbers
from Java, but the CDK can extract these from the auxiliary layer. These numbers
are those listed in the bond layer, but to use these in the CDK molecule class,
we need to mapping of the InChI atom numbers This method
is made available via the InChINumbersTools class:
Script 13.14 code/InChIAtomNumbers.groovy
oxazole = MoleculeFactory.makeOxazole();
long[] morganNumbers =
InChINumbersTools.getNumbers(
oxazole
);
for (i in 0..(oxazole.atomCount-1)) {
atom = oxazole.getAtom(i)
println atom.symbol +
" " + morganNumbers[i]
}
which outputs:
C 2
O 5
C 3
N 4
C 1
It is important to note that because these numbers are used in the connectivity layer, symmetry is broken in assignment of these numbers, allowing all atoms in, for example, benzene to still be uniquely identified:
Script 13.15 code/InChIAtomNumbersBenzene.groovy
benzene = MoleculeFactory.makeBenzene();
long[] numbers =
InChINumbersTools.getNumbers(
benzene
);
for (i in 0..(benzene.atomCount-1)) {
atom = benzene.getAtom(i)
atom.setProperty(
"AtomNumber",
"" + numbers[i]
)
}
which outputs:
C 1
C 2
C 4
C 6
C 5
C 3
The InChI atom numbers are shown in Figure 14.1.
References
- OpenEye, Smallest Set of Smallest Rings (SSSR) Considered Harmful, http://www.eyesopen.com/docs/toolkits/current/html/OEChem_TK-python/ring.html#smallest-set-of-smallest-rings-sssr-considered-harmful
- Figueras J. Ring Perception Using Breadth-First Search. JCICS. 1996 Jan;36(5):986–91. doi:10.1021/CI960013P (Scholia)
- Berger F, Gritzmann P, de Vries S. Minimum Cycle Bases for Network Graphs. Algorithmica. 2004 May 28;40(1):51–62. doi:10.1007/S00453-004-1098-X (Scholia)
- Hanser Th, Jauffret Ph, Kaufmann G. A New Algorithm for Exhaustive Ring Perception in a Molecular Graph. JCICS. 1996 Jan;36(6):1146–52. doi:10.1021/CI960322F (Scholia)
- Floyd RW. Algorithm 97: Shortest path. CACM. 1962 Jun 1;5(6):345. doi:10.1145/367766.368168 (Scholia)
- Morgan HL. The Generation of a Unique Machine Description for Chemical Structures-A Technique Developed at Chemical Abstracts Service. Journal of chemical documentation. 1965 May;5(2):107–13. doi:10.1021/C160017A018 (Scholia)